I lied!

I said I didn’t want to implement any linear algebra in Rust. Best to leave it to the experts! It seems I couldn’t resist the attraction.

Someone mentioned BLIS, and I fell into the rabbit hole. It’s an interesting linear algebra package, some of its specifics also fit ndarray better than regular BLAS does, so I had to keep reading.1

I found their papers (1) (2) and presentations (3). Really interesting! They present an efficient approach to implementing matrix multiplication and a whole “BLAS-like” suite of algorithms, by breaking it down into component algorithms.

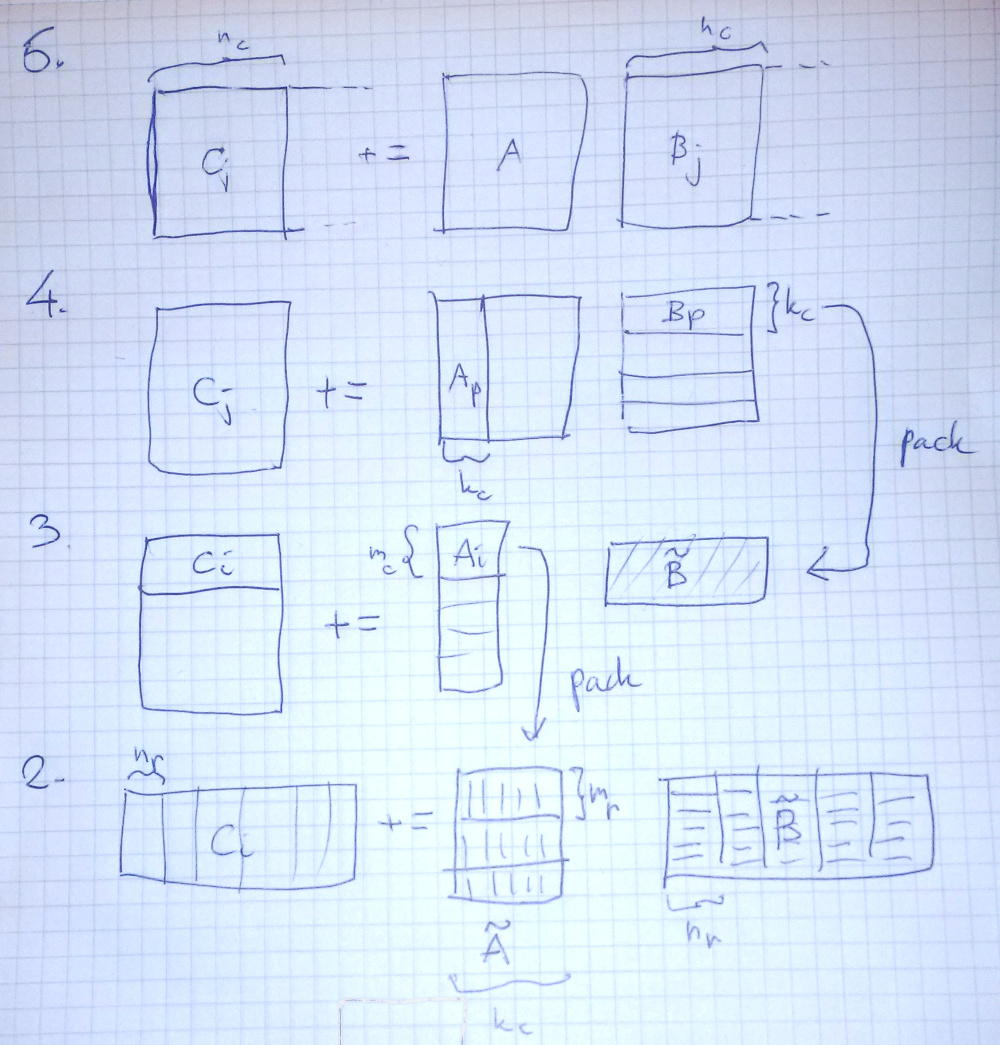
matrix splitting scheme Artist’sMadman’s impression of the matrix packing process. The numbers 5, 4, 3, 2, 1 are nested loops (5 the outermost) where the microkernel is looped over as #1. You could look at the real image, too.

In particular they have this image (from wiki) which shows well how they partition the matrices. With their scheme, it does not seem so hard after all to implement a good matrix multiplication.

At the core of it there’s just one matrix multiplication kernel, a microkernel, that takes as input two 4-by-k input columns of data and multiply-add it into a 4-by-4 result matrix.2

Like the BLIS people found out, this means that the core of the operation is quite small. The expert-optimized cores needed are reduced compared to earlier strategies. (They go on to reuse the microkernel for several related operations, such as the symmetric cases).

I had to try to write this in Rust. It’s not going to be revolutionary, but it’s going to be fun, and a heck of an improvement over a naive matrix multiplication algorithm. This algorithm packs the matrices into a form that’s efficient to process, then feeds it to the microkernel. Packing the data pays off already when the matrices are very small.

A 4-by-4 microkernel for f32

Never mind that the comment only partly explains the interface. Look how simple and stupid this is!

/// index ptr with index i
unsafe fn at(ptr: *const f32, i: usize) -> f32 {
    *ptr.offset(i as isize)
}

/// 4x4 matrix multiplication kernel for f32
///
/// This does the matrix multiplication:
///
/// C ← α A B + β C
///
/// + k: length of data in a, b
/// + a, b are packed
/// + c has general strides
/// + rsc: row stride of c
/// + csc: col stride of c
/// + if `beta` is 0, then c does not need to be initialized
#[inline(always)]
pub unsafe fn kernel_4x4(k: usize, alpha: f32, a: *const f32, b: *const f32,
                         beta: f32, c: *mut f32, rsc: isize, csc: isize)
{
    let mut ab = [[0.; 4]; 4];
    let mut a = a;
    let mut b = b;

    // Compute matrix multiplication into ab[i][j]
    unroll_by_8!(k, {
        let v0 = [at(a, 0), at(a, 1), at(a, 2), at(a, 3)];
        let v1 = [at(b, 0), at(b, 1), at(b, 2), at(b, 3)];
        loop4x4!(i, j, ab[i][j] += v0[i] * v1[j]);

        a = a.offset(4);
        b = b.offset(4);
    });


    macro_rules! c {
        ($i:expr, $j:expr) => (c.offset(rsc * $i as isize + csc * $j as isize));
    }

    // Compute C = alpha A B + beta C,
    // except we can not read C if beta is zero.
    if beta == 0. {
        loop4x4!(i, j, *c![i, j] = alpha * ab[i][j]);
    } else {
        loop4x4!(i, j, *c![i, j] = *c![i, j] * beta + alpha * ab[i][j]);
    }
}

I’m making a mockery of rust by using some simple macros for sixteenfold repetition and for unrolling the loop. (And yes, macros can ”capture” local variables like c![] does.) Apart from that, these are just some simple f32 operations.

With the kernel in place, “only” add the five nested loops around it, and it’s complete.

Now we turn to RUSTFLAGS="-C target-cpu=native" cargo build --release and we hope that the compiler can turn this into something decent!

This is what one iteration of the f32 kernel compiles to on my platform (AVX):

  vbroad xmm4,DWORD PTR [rsi]                  // a0
  vmovss xmm5,DWORD PTR [rax+0xc]              // b3
  vinser xmm5,xmm5,DWORD PTR [rax+0x8],0x10    // b2
  vinser xmm5,xmm5,DWORD PTR [rax+0x4],0x20    // b1
  vinser xmm5,xmm5,DWORD PTR [rax],0x30        // b0
  vmulps xmm4,xmm4,xmm5                             
  vaddps xmm3,xmm3,xmm4                             
  vbroad xmm4,DWORD PTR [rsi+0x4]              // a1
  vmulps xmm4,xmm4,xmm5                             
  vaddps xmm2,xmm2,xmm4                             
  vbroad xmm4,DWORD PTR [rsi+0x8]              // a2
  vmulps xmm4,xmm4,xmm5                             
  vaddps xmm1,xmm1,xmm4                             
  vbroad xmm4,DWORD PTR [rsi+0xc]              // a3
  vmulps xmm4,xmm4,xmm5                             
  vaddps xmm0,xmm0,xmm4

This is nice, even if this is far from optimal. I’ve put in comments where each word is loaded. The a0-3 go into separate vectors (nickname row[i]), and the b0-3 into one vector (xmm5), then we compute ab[i] += row[i] * b for i = 0..4.

Benchmark

To evaluate it, I plug it in to ndarray’s benchmarks. Ndarray can already use OpenBLAS, and it’s easy to plug in this new code too.

The benchmark problem is a matrix multiplication where A is 128-by-10000 and B is 10000-by-128.

Let’s see how they compare, the new code first:

test mat_mul_f32::mix10000         ... bench:  23,711,252 ns/iter (+/- 479,749)

And compare with OpenBLAS:

test mat_mul_f32::mix10000         ... bench:  11,583,222 ns/iter (+/- 377,390)

(Edit: Later I managed to improve the pure rust version to just 14,278,440 ns/iter see (1) and (2)!)

Uh oh OpenBLAS is good! And this is even when both are running with just one thread (OpenBLAS will otherwise automatically use multiple threads for this problem). We can compare the vitals (using perf stat) of the two runs, first our new code, then OpenBLAS. Note that these are not timing runs.

 # our gemm in Rust
 Performance counter stats for 'bench1-5a64c4157ddeecdb mat_mul_f32::mix10000 --bench':

       7763,353834      task-clock (msec)         #    0,999 CPUs utilized
                30      context-switches          #    0,004 K/sec
                 0      cpu-migrations            #    0,000 K/sec
           262 780      page-faults               #    0,034 M/sec
    20 762 623 489      cycles                    #    2,674 GHz                      (83,32%)
     2 715 196 375      stalled-cycles-frontend   #   13,08% frontend cycles idle     (83,32%)
       944 555 212      stalled-cycles-backend    #    4,55% backend  cycles idle     (66,64%)
    56 070 804 002      instructions              #    2,70  insns per cycle
                                                  #    0,05  stalled cycles per insn  (83,36%)
       835 478 687      branches                  #  107,618 M/sec                    (83,37%)
        14 738 790      branch-misses             #    1,76% of all branches          (83,36%)

       7,768514309 seconds time elapsed

 # OpenBLAS
       4200,153498      task-clock (msec)         #    0,999 CPUs utilized          
                24      context-switches          #    0,006 K/sec                  
                 6      cpu-migrations            #    0,001 K/sec                  
           259 575      page-faults               #    0,062 M/sec                  
    11 101 041 529      cycles                    #    2,643 GHz                      (83,29%)
     3 851 326 526      stalled-cycles-frontend   #   34,69% frontend cycles idle     (83,34%)
     1 295 653 986      stalled-cycles-backend    #   11,67% backend  cycles idle     (66,69%)
    23 169 366 472      instructions              #    2,09  insns per cycle        
                                                  #    0,17  stalled cycles per insn  (83,34%)
       379 432 628      branches                  #   90,338 M/sec                    (83,34%)
         1 480 386      branch-misses             #    0,39% of all branches          (83,34%)

       4,203170924 seconds time elapsed

The autovectorized result of our microkernel isn’t too shabby. There’s some good news here. Our code is maxing out the one core pretty well. Relatively few cycles idle, so we’re doing something right. It should be no surprise that OpenBLAS uses fewer instructions, they probably emit them with a bit more care (hand coded assembly.)

Our code can be a good fallback for the cases that OpenBLAS doesn’t handle, in particular the general stride cases.

Desserts

Now we can use this! The crate is matrixmultiply (docs) and implements f32 and f64 matrix multiplication in Rust. Input and output matrices may have general strides (this means that it has great flexibility in memory layouts of the operands)!

I guess the result kind of sucked, since it didn’t beat OpenBLAS? I don’t think so, they are the experts, their work is based on code that goes decades back, so we can’t be surprised. I even told you so, stick with the experts.

If we don’t do that, there’s plenty of avenues to develop matrixmultiply. 1) Find a plain rust formulation that autovectorizes better, 2) Try unstable simd support 3) Try inline asm! Following the methodology to only optimize the microkernel, it shouldn’t be too hard to improve this immensly with one of those techniques. 90% or more of the work is spent inside the microkernel.

Another interesting idea would be to use the blocked algorithm to implement a dense-sparse matrix multiplication.

My lie wasn’t so bad. It’s not like I’m setting out to implement all of linear algebra. No promises if it’s going to continue! In the meanwhile, this implementation is perfectly reusable, general, and has a structure that makes it easy to improve by parallelization or optimization.

We have so much work to do! I would like to get in touch with others that are interested. We need a place to gather, do you know about the irc channel #rust-machine-learning on irc.mozilla.org?

One “simple” thing on my mind that requires people to gather to collaborate is to further the state of numerical traits in Rust. Even code generic over just f32, f64 is rather unpleasant!

End

  1. BLIS was a better fit for ndarray because it 1) allows arbitrary-ish row and column stride for input matrices, and 2) defaults to 64-bit indices, which means we have no corner cases (larger than 32-bit arrays) that need fallback. ↩

  2. 4-by-4 is an example, and the kernel may instead by 8-by-4, or 8-by-8 etc. ↩